Finding Matrices that you can multiply wrong, right
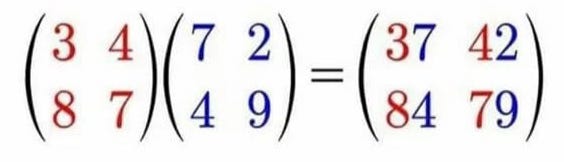
My codegolf.stackexchange post
Github Repository with experiments
I went on an adventure finding NxN matrices and where .
Symbolic work
First of all, for a given candidate A, B is fixed:
One approach is to take the eigendecomposition of A.
From before,
This shows that A, B share eigenvectors Q, and their eigenvalues are assosciated by
Interestingly, this proves that AB = BA, ie our matrices commute!
We can calculate the determinant of B as This is very suggestive, but doesn't immediately yield a way to pick a matrix A such that B is small positive integers.
Because A and B share eigenvectors, B can be written as a linear combination of . For example,
We observe that , so . In this case B is forced to be an integer matrix because it is possible to write B as an integer polynomial of A. If we can find large matrices where is an integer polynomial of , then that might provide an efficient solution.
Finally, if we write as , then we can see some simplifications. , so B is an integer matrix as long as the determinant of E divides 10. With this E representation, our problem can become to find an integer matrix E such that
(Occasionally this will fail if an entry of )
This represents an improvement, because once we find a [0-9] matrix E with determinant (such as by random search), then if there are only a small number of negative entries in we can run determinant-preserving transformations on E such as permuting rows to move those negative entries onto the diagonal, where they are made positive by the
In addition, there is a name and wikipedia page for matrices like where the off diagonal entries are all positive: A Metzler Matrix. Further literature search in that direction might bring up an efficient way to generate positive integer matrices with a determinant whose inverses are Metzler Matrices.