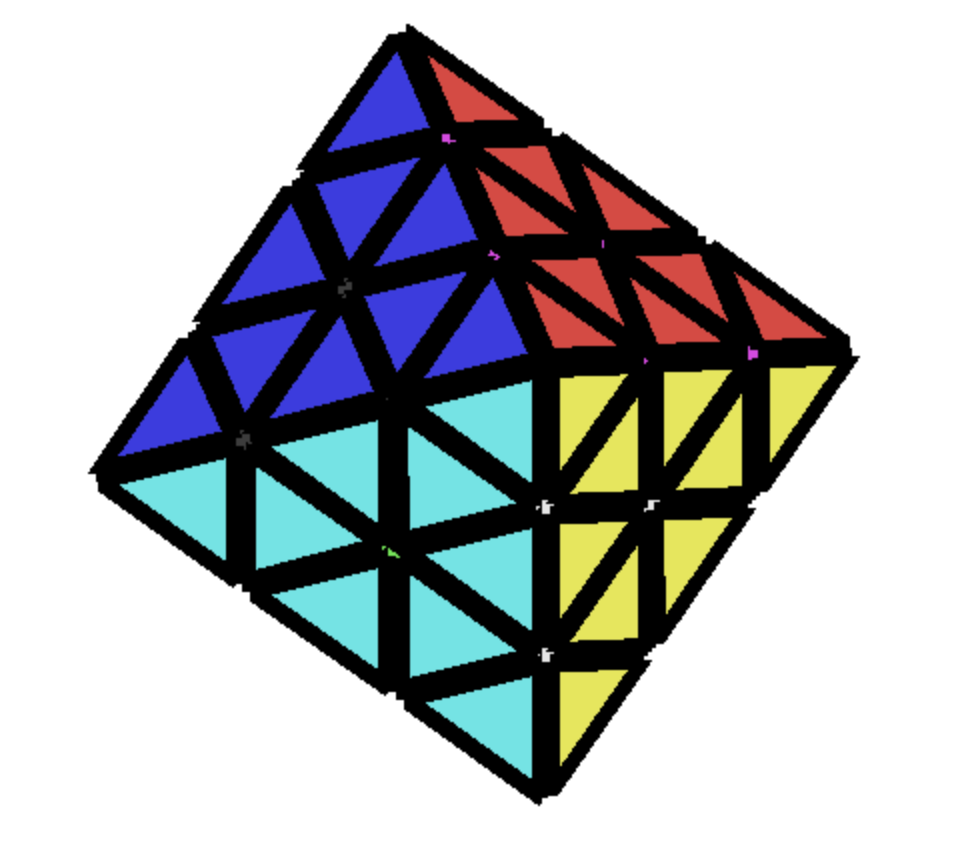
The in browser, playable rubiks cubes, including a pyraminx and a face turing octahedron, are currently hosted here. Hopefully this post will eventually get to explaining how they work
Rubiks cubes are fascinating, and I've been working on writing a post about solving them for a while. At first, I thought that the post would be about solving them, and the draft of that post is at (link) but I quickly realized that the post about solving them needed playable, embedded widgets where the reader could try the techniques in question.
PyObject <module 'scipy' from '/opt/hostedtoolcache/Python/3.10.19/x64/lib/python3.10/site-packages/scipy/__init__.py'>The unfinishable post in question
Thus, this post started, a prequel of sorts, about how to embed a twisty cube widget in a website. It becomes a bit of a journey.
I started off implementing a copy of Simon Tatham's "Twiddle", which is a simplified puzzle with rubiks like motion. Instead of stickers on cublets, it just has 16 tiles in a square, with the ability to turn 3x3 sub-sets of the puzzle by 90 degrees. I elected to represent the state of the puzzle and the moves as 16 x 16 permutation matrices. Then, I could apply a move by simply multiplying it with the state. Render the puzzle by multiplying the state with a "piece location" matrix.
import numpy as np
import matplotlib.pyplot as plt
import sys
state = np.eye(16)
display_matrix = []
for i in range(4):
for j in range(4):
display_matrix.append([j, -i])
display_matrix = np.array(display_matrix) - np.mean(display_matrix, axis=0, keepdims=True)
def show(state):
[plt.text(x, y, str(i), ha='center', va='center', fontsize=16)
for i, (x, y) in enumerate(state @ display_matrix / 5 + .5)]
show(state)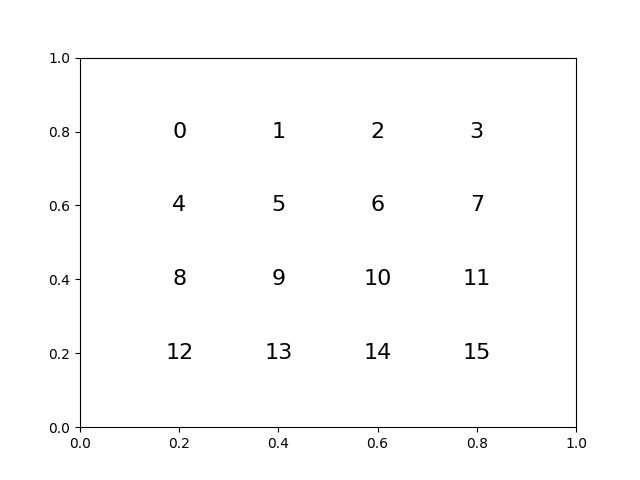
For a start, we just hand write the permutation for a single move
move = (np.
array([[0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.],
[0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]]))
show(move @ state)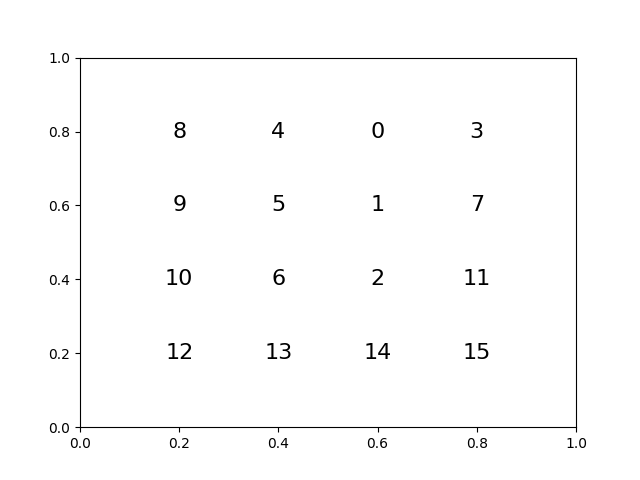
This successfully twisted the top left square!
This is where the magic starts, and the justification arrives for representing moves via matrices. How are we going to animate this move? Easy! if we want the move to take 2 frames, we just take the square root of move!
from scipy.linalg import logm, expm
show(expm(logm(move) / 2) @ state)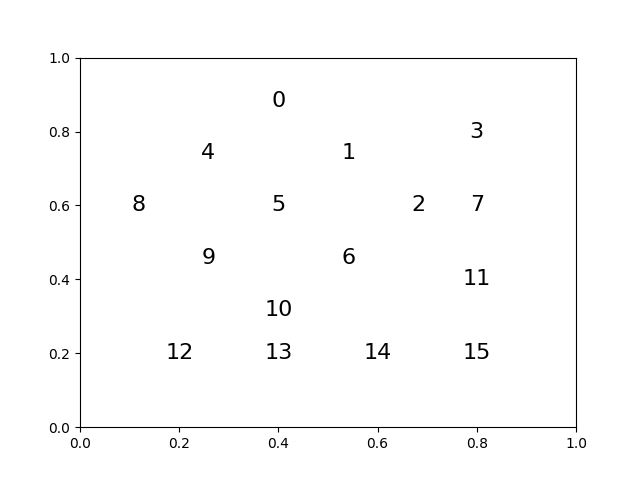
This works for any fraction of a turn we want, allowing easy smooth animation of any permutation.
Now, writing out that matrix move sucked, and it's only going to get worse to do manually as we scale up the sticker count: Instead, lets let a computer find it!
The plan is to create a general function that takes a set of points (such as the one in our display matrix, or a subset corresponding to a move) and returns all the possible rotations of the the points that correspond to permutations of the points, by finding all solutions to
where is the display matrix we computed earlier, is a permutation, and is a physical rotation.
This can be done efficiently by a backtracking solve. Let be a prefix matrix, like
Think of this as takes the first 5 rows of
Then, if , we know that
By contrapositive, if there are no solutions Q to , there are no solutions to
This lets us use a standard recursive iterator through all permutations, but with pruning whenever is unsolvable.
def DQ_AD_solve(D):
eye = np.eye(len(D))
def feasible(permutation_so_far):
if ( np.abs(np.linalg.norm(D[len(permutation_so_far) - 1]) - np.linalg.norm(D[permutation_so_far[-1]])) > 0.001):
return False
P = eye[: len(permutation_so_far)]
PA = eye[permutation_so_far]
Q, residuals, _rank, _singular_values = np.linalg.lstsq(P@D, PA@D)
if np.abs(np.linalg.det(Q) + 1) < .001:
return False
if len(permutation_so_far) == len(D):
permutations.append(PA)
rotations.append(Q)
return False
return len(residuals) == 0 or (np.max(np.abs(residuals)) < 0.0001).item()
def recursive_permutations(permutation_so_far):
for i in range(len(D)):
if not i in permutation_so_far:
continuation = permutation_so_far + [i]
if feasible(continuation):
recursive_permutations(continuation)
permutations = []
rotations = []
recursive_permutations([])
return permutations, rotations
global_perms, global_rotations = DQ_AD_solve(display_matrix)
[print(np.argmax(perm, axis=0)) for perm in global_perms][ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]
[12 8 4 0 13 9 5 1 14 10 6 2 15 11 7 3]
[ 3 7 11 15 2 6 10 14 1 5 9 13 0 4 8 12]
[15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0]
This global_perms array is super useful, because it not only gives all the moves that rotate the whole puzzle, it also gives all the sub-moves of the puzzle by computing A @ move @ A.T for all the symmetries A found by DQ_AD_solve
frames = 64
for j in range(frames):
for i, element in enumerate(global_perms):
plt.subplot(2, 2, i + 1)
show(expm(1/16 * j * logm(element @ move @ element.T)))
Notice that we were able to combine 3 moves (rotate the whole puzzle, turn a piece, then rotate the whole puzzle back) and our animation approach fuses this into a single rotation.
In addition, for future puzzles, we won't need to write out move by hand: instead, we will take a subset of the display matrix corresponding to that part we want to rotate, and appy DQ_AD_solve to that.
That's enough to implement Twiddle! There's an interactive version here. For the interactive version, I swapped out the matplotlib display for pygame, and then threw it all into the browswer using Pyodide, which is a python interpreter (with scipy, pygame, and numpy!) compiled to web assembly.
Next, it's time to move to the third dimension! With the groundwork we've laid, it's super easy.
We build a display matrix for a 3x3 rubiks cube, and record the colors of the permutable pieces since rubiks cube uses colors, not numbers.
import itertools
colors = []
display_matrix = []
for sticker in itertools.product(* [range(5)] * 3):
sticker = np.array(sticker)
if np.sum(sticker == 0) + np.sum(sticker == 4) == 1:
colors.append(.5 + .5 * (0 - (sticker == 0) + (sticker == 4)))
display_matrix.append(sticker)
display_matrix = np.array(display_matrix) - np.mean(np.array(display_matrix), axis=0, keepdims=True)
colors = np.array(colors)
state = np.eye(54)
def show(state):
locations = state @ display_matrix
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
ax.set_zlim(-2, 2)
ax.scatter(locations[:, 0], locations[:, 1], locations[:, 2], c=colors, s=800, alpha=1)
show(state)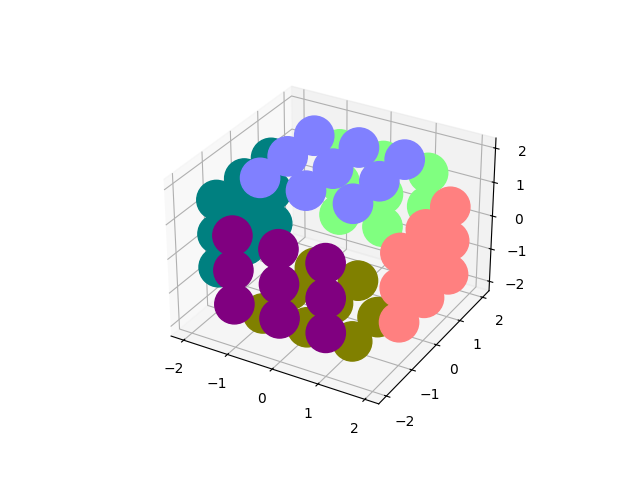
I use the global permutations to rotate the cube along any of its axes
global_perms, global_rotations = DQ_AD_solve(display_matrix)
for i, element in enumerate([1, 12, 4, 9]):
element = global_perms[element]
for j in range(frames // 4):
state = state@expm(1/16 * logm(element))
show(np.real(state))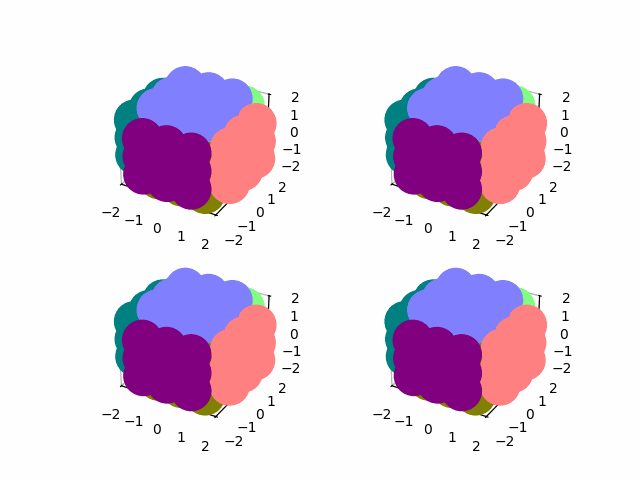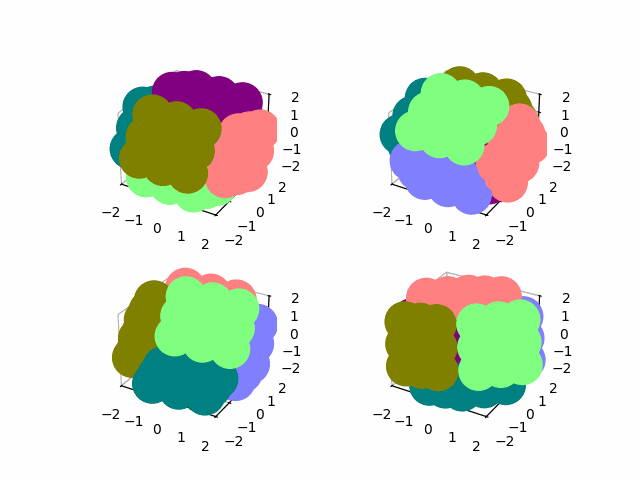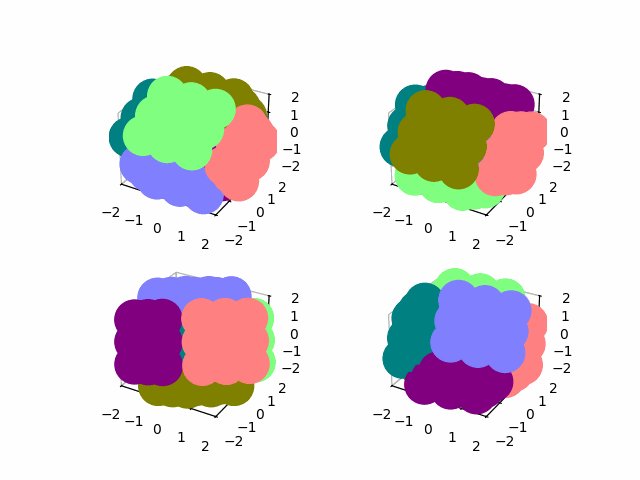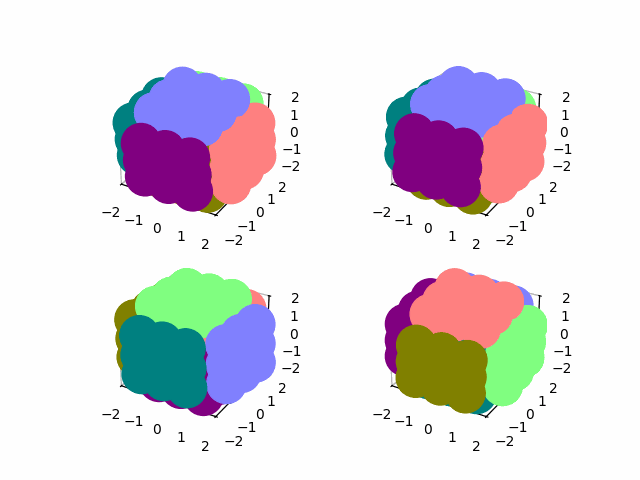
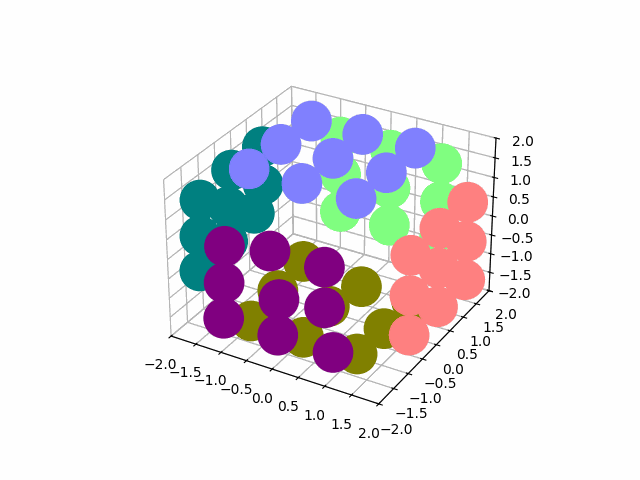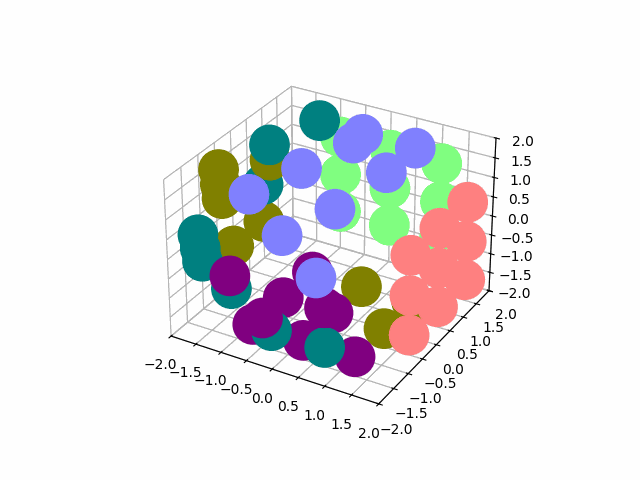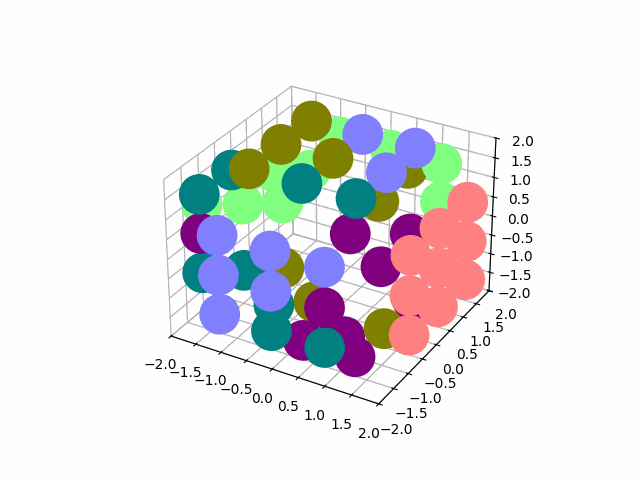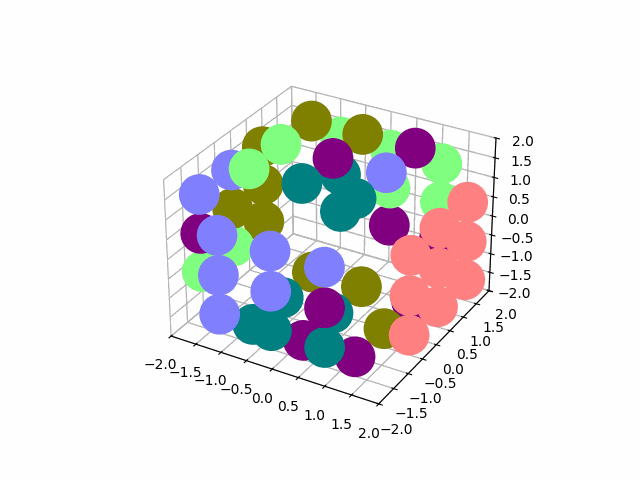
And I use the permutations of a subset of the cube to rotate a single slice. As before, we compute a single "move" permutation, and then get all the moves via matricies of the form element @ move @ element.T
slice_perms, slice_rotations = DQ_AD_solve(display_matrix[:21])
move = np.eye(54)
move[:21, :21] = slice_perms[1]
for i, element in enumerate([1, 3, 4, 9]):
element = global_perms[element]
for j in range(frames // 4):
state = state@expm(1/16 * logm(element @ move @ element.T))
show(np.real(state))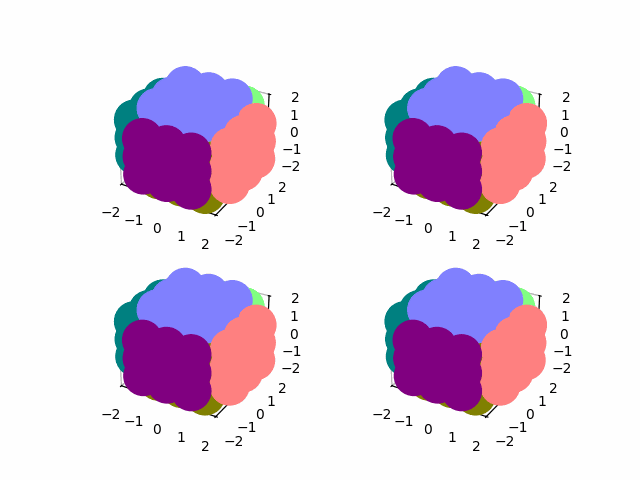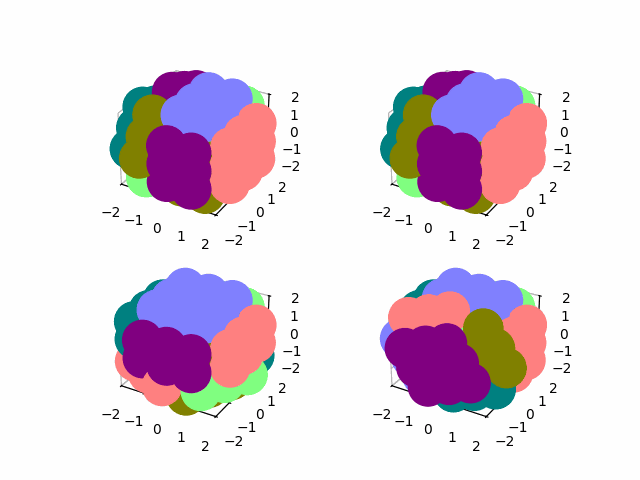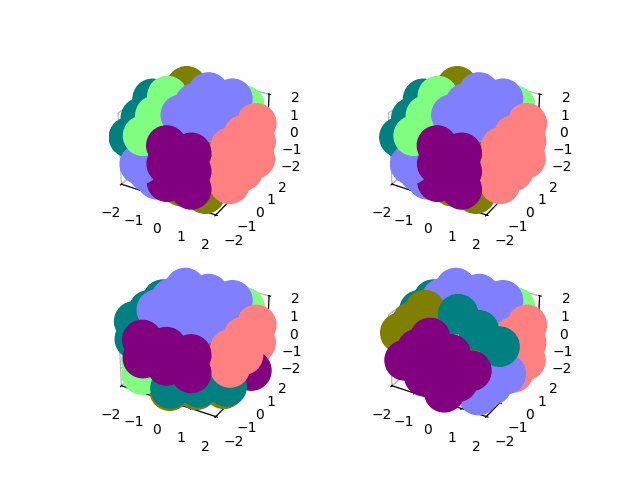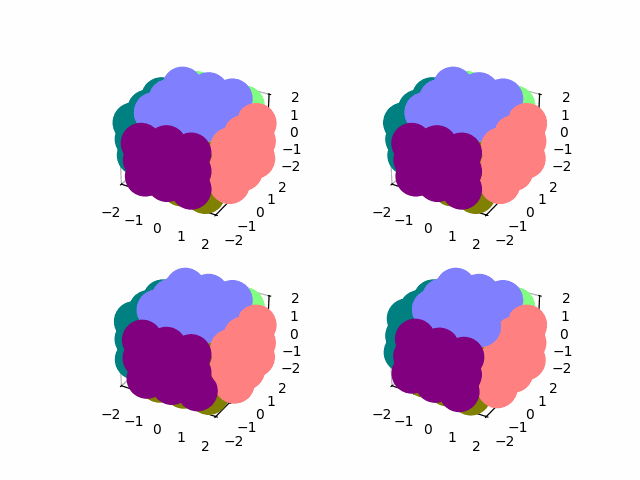
The playable version of this rubiks cube is here
Now, this is a standard rubiks cube. If we want to get a variant, it's as simple as selecting a different subset of the points to be the turnable slice.
re_order = np.argsort(np.sum(display_matrix, axis=1))
display_matrix = display_matrix[re_order]
colors = colors[re_order]
state = np.eye(54)
global_perms, global_rotations = DQ_AD_solve(display_matrix)
slice_perms, slice_rotations = DQ_AD_solve((display_matrix)[:18])
move = np.eye(54)
move[:18, :18] = slice_perms[1]
for i, element in enumerate([1, 3, 4, 9]):
element = global_perms[element]
for j in range(frames // 4):
state = state@expm(1/16 * logm(element @ move @ element.T))
show(np.real(state))