By Construction ICON
if we build an network that is inverse consistent by construction, then penalize it with the ICON error, how regularized is it? Does it become regularized by adding in noise?
notebook for byconstructionICON
results depend heavily on loss
Blurred SSD ConstICON
Blurred SSD NoReg
SSD ConstICON
SSD_only_interpolated_consticon
Simplified progressive train pipeline
Train the classic
inner_net = icon.FunctionFromVectorField(networks.tallUNet2(dimension=3))
for _ in range(2):
inner_net = icon.TwoStepRegistration(
icon.DownsampleRegistration(inner_net, dimension=3),
icon.FunctionFromVectorField(networks.tallUNet2(dimension=3))
)network end to end, then tack on an extra step at the final resolution.
inner_net = icon.FunctionFromVectorField(networks.tallUNet2(dimension=3))
for _ in range(2):
inner_net = icon.twostepregistration(
icon.downsampleregistration(inner_net, dimension=3),
icon.functionfromvectorfield(networks.tallunet2(dimension=3))
)
inner_net = icon.twostepregistration(
inner_net, icon.functionfromvectorfield(networks.tallunet2(dimension=3))
)this second step is trained using only half res gradicon but the same accurate finite differences
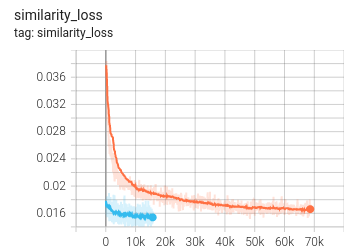
performance:
dice: tensor(0.7089)
mean folds: 0.17333333333333334calculation notebook
Paper work:
Convergence argument: I don't think that the o
Tag on: for both end to end and progressive, tag on fine tuning
Add a few sentences explaining that large channel counts at low resolution are basically free.
immediate todo: put sparse into master
Marc's paper that he is curious about
https://www.sciencedirect.com/science/article/pii/S1361841522000858
Mattias Heinrich's paper contains ANT, elastix lung results
how does it do so good?
Back to Reports