Atlas registration progress
At low resolution
Since last time, found that I could not train ICON_atlas loss to match performance of ICON on OAI knees: second step of multiscale training failed as folds ran away, lambda increased to infinity.
Outreach:
Presenting same powerpoint from group meeting last week to funky bunch on wednesday. Several people from Kitware's AI team coming: anything I should make sure to include?
Follow up to "New approach to patchwise registration"
Wanted to setup for applying Instant Neural Graphics Primitives to neural registration fields. To do this, I needed a valid regularization proceedure. Started with this approach:
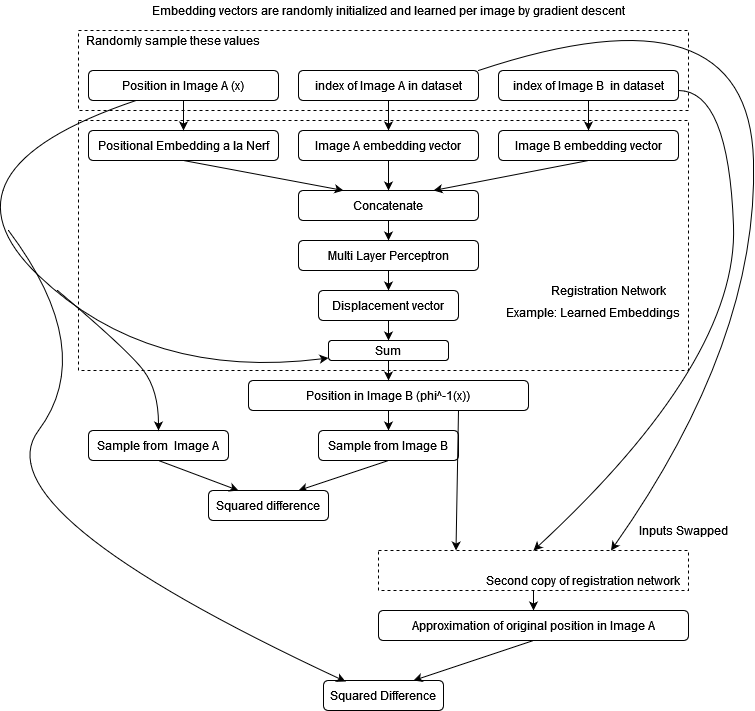
Which then doesn't work: produces very irregular mappings or identity map:
New approach: Use torch.autograd to compute spatial gradients of node "Approximation of original position in Image A, - Position in Image A" with respect to node "Position in Image A"
Square these partial derivatives and minimize the result. This is inspired by the gradient penalty for GANS espoused in When do GANS actually converge which we discussed a while back: Each sample forces a neighborhood around it to be near zero, instead of just a single point.
FOR A SINGLE PAIR, THIS WORKS FOR REGISTRATION!
Image A
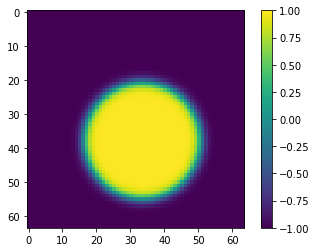
Image B
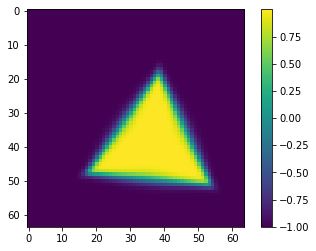
Grid

Warped B
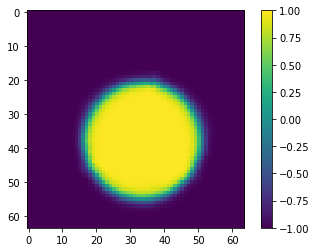
GradientICON
While getting the above to work, I was impressed enough with the performance of the Jacobian penalty on the Inverse Consistency term to try it back on the standard convolutional ICON.
I computed the jacobian using finite differences instead of torch.autograd since that was more convenient, and it's only through linear interpolations, so finite differences are usually exact anyways.
delta = .001
if len(self.identityMap.shape) == 4:
dx = torch.Tensor([[[[delta]], [[0.]]]]).to(config.device)
dy = torch.Tensor([[[[0.]], [[delta]]]]).to(config.device)
direction_vectors = (dx, dy)
elif len(self.identityMap.shape) == 5:
dx = torch.Tensor([[[[[delta]]], [[[0.]]], [[[0.]]]]]).to(config.device)
dy = torch.Tensor([[[[[0.]]], [[[delta]]], [[[0.]]]]]).to(config.device)
dz = torch.Tensor([[[[0.]]], [[[0.]]], [[[delta]]]]).to(config.device)
direction_vectors = (dx, dy, dz)
for d in direction_vectors:
approximate_Iepsilon_d = self.phi_AB(self.phi_BA(Iepsilon + d))
inverse_consistency_error_d = Iepsilon + d - approximate_Iepsilon_d
grad_d_icon_error = (inverse_consistency_error - inverse_consistency_error_d) / delta
direction_losses.append(torch.mean(grad_d_icon_error**2))
inverse_consistency_loss = sum(direction_losses)This works great in 2d, solving the hollow triangles circles benchmark in 2 minutes instead of ~ an hour, and with more reliable and higher quality final results:
GradientICON in 3D
Trains like a dream with not much fussing even at batch size 1, 160 x 384 x 384.
Step 1 (40 x 96 x 96): DICE 66
Step 2 (80 x 192 x 192): DICE 71.3
Step 3 (160 x 384 x 384): DICE 73.3
Back to Reports